n阶对称矩阵权威发布_矩阵a 1(2024年12月精准访谈)
Jordan标准型在矩阵问题中的应用 Jordan标准型在矩阵理论中有着广泛的应用,尤其在解决复杂矩阵问题时显得尤为有效。以下是几个应用Jordan标准型的典型例子: 应用Jordan标准型的三段论法 如果矩阵问题的条件和结论在相似关系下不改变,可以先证明结论对Jordan块成立,再证明对Jordan标准型成立,最后再证明对一般的矩阵也成立。 例如,设n阶矩阵A的特征值全为1或-1,证明A与A相似。 设n阶矩阵A的特征值全为1,证明VkEN,A与A相似。 求矩阵B,使得A=B,其中A=31-15。 设A∈Mn(C)且A可逆,证明:VmEN,存在BE Mn(C)使得A=Bm。 设A∈Mn(C),证明:存在n阶复对称矩阵B,C,使得A=BC,并且可以指定BC中任何一个为可逆矩阵。 设A∈Mn(C),证明:存在阶非异复对称矩阵Q,使得Q-AQ=A。 頥ˆ駔芯rdan标准型对问题进行化简 设A,B为n阶矩阵,且AB=BA=0,(A)=F(A),证明:r(A+B)=r(A)+r(B)。 设AB分别是m,n阶矩阵,证明:矩阵方程AX=XA只有零解的充要条件是A,B无公共的特征值。 设A,B分别是m,n阶矩阵,C是m㗮矩阵,证明:矩阵方程AX-XB=C存在唯一解的充要条件是A,B无公共的特征值。 젩‡‡用Jordan块作为测试矩阵 求证:存在71阶实方程A,使得:201920181949 A0+++A+11= 2019 2018 2019。 设m∈N,证明:Vn,lN,存在m阶实方阵X,使得X"+X'=m+。 利用Jordan标准型研究矩阵的性质 设A为n阶复方阵,证明:A相似于分块对角矩阵diag(BC),其中B是幂零矩阵,C是可逆矩阵。 设A∈Mn(K),证明:A的极小多项式的次数小于等于r(A)+1。 通过这些例子可以看出,Jordan标准型在解决矩阵问题时具有强大的工具性,能够帮助我们简化复杂的计算和证明过程。
特征值与相似对角化矩阵的奥秘 Ÿ 矩阵能够相似于对角矩阵的关键在于它是否拥有足够多的线性无关的特征向量。‘ 特征值是决定特征向量存在与否的关键因素。当矩阵的特征值互不相同时,通常意味着每个特征值都对应一个独立的特征向量。𑠥œ訿™种情况下,矩阵有足够的线性无关的特征向量来形成一个完整的基,从而能够实现对角化。 具体来说,如果n阶方阵A有n个不同的特征值,那么每个特征值都将对应一个特征向量,并且这些特征向量由于特征值的不同而自然线性无关。„ 这样,A就有n个线性无关的特征向量,满足了相似对角化的充要条件。 相反,如果矩阵的特征值有重根,即存在相同的特征值,那么情况就会变得复杂。�—Œ即便某个特征值重复出现,只要它对应的线性无关特征向量的个数等于该特征值的重数,矩阵仍然可以相似对角化。但如果线性无关特征向量的个数少于特征值的重数,矩阵就不能对角化。 不同的特征值能够确保矩阵具有足够的线性无关的特征向量,从而使得矩阵能够相似于对角矩阵。然而,这只是一个充分条件,不是必要条件。ˆ 实对称矩阵就是一个例外,它总是可以相似对角化,不论其特征值是否相同。
全国大学生线性代数期末考试试卷解析 选择题(每题3分,共15分) 1. 设A, B为n阶可逆方阵,则下列等式恒成立的是(D) A. (AB) = A-1B-1 B. (AB) = A*B* C. (AB)-1 = B-1A-1 D. (A+B) = B* + A* 2. 设A为m㗮型矩阵,则下列命题中正确的是(D) A. 若R(A)=m, 则A可逆 B. 若R(A)=n, 则A可逆 C. 若A行满秩, 则A可逆 D. 若A满秩, 则A可逆 3. 设A, B为n阶方阵,则下列命题中正确的是(D) A. R(A)-R(B) ≤ R(A-B) B. R(A)+R(B) ≤ R(A+B) C. R(A)R(B) ≤ R(AB) D. R(A, B) ≤ R(A)R(B) 4. 设向量组 a, a… am (m≥2)线性无关,B, B2…,B为与a, a2… 同维的向量组。下列命题正确的是(D) A. 若m=n,则1, B2… Bn与a1, a2, …, am等价 B. 若B1, B2, …, B可由a, a2…, am线性表示,则n≤m C. 若a1, a2, … am可由B1, B2, …, B线性表示,则m≤n D. 若B1, B2… Bn线性无关,则B1B2…, B与a1, a2, …, am等价 5. 设A为n阶对称矩阵(n≥2)。下列命题正确的是(C) A. A有n个不同的特征值 B. A的任意n个不同的特征向量均互相正交 C. A的任意两个不同特征值下的特征向量一定互相正交 D. A的任意两个互相正交的特征向量一定属于不同的特征值 填空题(每题3分,共15分) 6. 排列(1375624)的逆序数t(1375624)= 4 7. 设A为3阶方阵,且A=3,则2A-1-A= 2/3 8. 已知向量(1,-2,1)与向量(-2,t,1)正交。则t = -3 9. 若含有5个未知量4个方程的非齐次线性方程组有3个线性无关的解,且没有4个线性无关的解,则其系数矩阵的秩为 3 10. 若方阵A满足2A2-3A=-4E,则(3A-2E)-1= -4/5 解答题(共70分) 11. 计算行列式:|1 -3 2| |4 -2 3| |5 2 1| = -8 12. 求矩阵A的逆矩阵:其中 A = |2 2 -1| |-1 3 -2| |0 0 0| = -1/6 |3 -2 -1| |-1 4 -3| |0 0 0| 13. 解线性方程组:|3x - x + 2x + 2x = 1| |x - 2x + 3x - 3x = 2| |2x + x - x + 5x = -1| 解得 x = [7/9] [8/9] [4/9] [5/9] 14. 求向量组a1=(1,0,1,1), a2=(0,-1,1,2), =(-1,2,1,-5), =(-1,3,2,-7), =(2,1,3,0)的一个含有的极大线性无关组,并将其余向量用该线性无关组表示。解得:极大线性无关组为 (a4) = (-1, 3, 2, -7),
实对称矩阵的那些事儿 簧Ÿ驘™个东西,看起来很平常,但其实背后藏着不少秘密。首先,实对称矩阵可以相似对角化,这不过是表象。真正重要的是,n阶实对称矩阵有n个线性无关的特征向量。换句话说,每个特征值都有相应数量的线性无关特征向量。 更进一步,实对称矩阵的不同特征值的特征向量是正交的。这意味着你可以用正交矩阵来相似对角化。正交矩阵就是由n个线性无关的特征向量经过施密特正交化后拼成的。 对于初学者来说,很容易只看到表象,而忽略本质。这样在做题时会吃亏,比如例8.14和例8.15。所以,我们应该时刻反思解题步骤中用到的是哪个知识点,并在多个练习结束后把知识点串成串⣀‚看到已知条件就能形成连锁反应,灵活挑选当下所需的知识点,解题自然就变得行云流水Ž。 总之,实对称矩阵不仅仅是一个可以相似对角化的矩阵,它背后隐藏着更深层次的数学原理。掌握这些原理,才能更好地理解和应用实对称矩阵。
396经综数学重点攻略,快来看看吧! 嘿,还在死磕数三吗?396经综数学的重点已经为你整理好了!快来看看吧! 微积分部分 极限的定义和性质:这可是常考内容,主要考察极限是否存在。 计算极限:各种求极限的方法,特别是6类未定型极限。 连续和间断点:分段函数和无意义点的考察。 无穷大无穷小阶数比较:了解不同阶数的比较方法。 导数:定义、几何应用、计算(一阶二阶为主,n阶也要掌握),特别是莱布尼茨公式,求高阶导数时会用到。 积分:定义、性质、不定积分的计算、定积分的计算、几何应用。 多元函数:求偏导(一阶或二阶)、偏导几何应用。 数列极限:了解数列极限的概念和计算方法。 求旋转体体积:掌握旋转体体积的计算公式和方法。 反常积分:反常积分的证明不用看。 概率论部分 概率计算:基本的概率计算方法。 分布函数:了解分布函数的概念和性质。 概率密度:掌握概率密度的计算方法。 常见分布:了解常见的概率分布类型。 二维随机变量分布:基本概念,离散型为主。 随机变量函数的分布:了解随机变量函数的分布计算方法。 随机变量的数字特征:掌握随机变量的各种数字特征。 线性代数部分 行列式计算:行列式的计算方法。 余子式:概念和计算方法。 矩阵:矩阵的计算、矩阵方程、逆矩阵、伴随矩阵。 向量线性相关性:了解向量的线性相关性。 秩:掌握秩的计算方法。 齐次/非齐次方程组的解:了解方程组的解法。 极大向量无关组:了解极大向量无关组的概念。 同解、公共解:了解同解和公共解的概念。 (反)对称矩阵:了解对称矩阵和反对称矩阵的概念。 赶紧收藏起来,按照这些重点来复习吧!祝大家考试顺利!–✨
【线代】Mr.Strang镇楼 9.斐波那契数列 二阶差分方程转为一阶方程组 矩阵分解得特征值(决定增长速度,太漂亮了,黄金分割线[苦涩])特征向量 100次方,最大项近似,其余忽略。(线性近似) 10.微分方程 n阶微分方程转化为n阶向量方程(n*n矩阵) 特征值特征向量分解,A—拉姆达I=0 根据特征值状态判断矩阵稳定状态(也就是矩阵中包含的信息,函数图像稳定状态) 矩阵稳定: (1)一个特征值=0,另外其他特征值(实数部分Re)<0 (2)两个特征值都<0(行列式>0),解收敛 矩阵不稳定:任意特征值(实数部分Re)>0,解不收敛(发散) 11.矩阵对角化 针对原方程组有两个相互影响的函数组成(耦合),特征值和特征向量作用是解藕,就是对角化。 对角矩阵∧,变量独立,各导各的。 12.矩阵指数 指数展开成幂级数,运用泰勒级数,几何级数,级数收敛得到求逆公式成立,对角线指数收敛于0 13.马尔科夫矩阵 性质:(1)所有元素>=0(2)每列相加=1 有一个特征值=1,其他特征值绝对值<1 Uk=A^kU。(按系数和特征值展开,在迭代中趋于0) 稳态:Uk趋于初始条件U。 应用于人口迁移问题(加利福尼亚州和马塞诸塞州,小郭和我最喜欢的阿美利卡州[允悲]) 14.投影 有标准正交基(中版教材的“极大无关组”概念) 15.傅立叶级数(周期函数) 针对函数连续情况做积分(点积) 傅立叶级数公式可以展开到正交基上 16.对称矩阵(正定性) 本质是一些相互垂直的投影矩阵的组合 特征值和特征向量矩阵分解 “性质好的矩阵” 实矩阵 A=A转置 复矩阵 实数部分对称,复数部分围绕对角线共轭 17.正定矩阵(所有特征值为正数的对称矩阵) 18.复数矩阵 酉矩阵(n阶方阵,列向量正交,单位向量,计算要共轭转置) 19.傅立叶矩阵 复数求内积(共轭后点乘) 欧拉公式的几何意义 傅立叶快速变换(递归,修正(列向量奇偶排列)+置换(计算机算法优化cs人狂喜[嘻嘻]) 20.半正定矩阵 一阶导数,二阶导数,主轴定理(矩阵分解)对称矩阵对角化 21.相似矩阵(做了基变换) 孤儿矩阵(只等价于自己) 若尔当定理(分块) 22.奇异值分解(SVD) 对角矩阵,A对行空间基做变换=列空间伸缩 四大空间标准正交基 23.线性变换条件(投影,旋转,伸长)其中平方,向量平移都不行력F•𐦱‚导(函数输入输出,投影到直线,向量投影到基向量)得到变换矩阵A 24.图像压缩 JPEG傅立叶变换基 小波基(平滑截断,压缩视频) 变换(换基换视角) SVD奇异值压缩原理:降维(完美基) 25.左右逆 伪逆(针对奇异(不可逆)矩阵)矩阵分块,取其中可逆的做逆,近似思想。 完结撒花~[送花花] 今天刚好是Mr.Strang90大寿生日[蛋糕] 再次祝您身体健康,寿比南山,平安喜乐,长命百岁[蜡烛] 我爱线代[心]线代爱我[心]线代万岁[互粉]
高等代数第五版教材+辅导与习题解答PDF š 高等代数第五版教材+辅导与习题解答 – 目录 第一章 多项式 数域 元多项式 整除的概念 最大公因式 因式分解定理 重因式 多项式函数 复系数与实系数多项式的因式分解 有理系数多项式 多元多项式 对称多项式 习题 补充题 第二章 行列式 引言 排列 n阶行列式 n阶行列式的性质 行列式的计算 行列式按一行(列)展开 克拉默法则 拉普拉斯定理ⷨጥˆ—式的乘法规则 习题 补充题 第三章 线性方程组 消元法 n维向量空间 线性相关性 矩阵的秩 线性方程组有解判别定理 线性方程组解的结构 元高次方程组 习题
华南数学考研,380+分秘籍! Ÿ华南师范大学903的考试内容今年依然涵盖了数分下册的最后几章,很多同学可能会忽视这一点,所以正在准备25级考研的同学们一定要重视起来,不要只复习前面的章节哦。 š数分部分: 泰勒公式 幂级数的收敛半径 隐函数求导 重要极限 二重积分坐标变换 第二型曲面积分 特殊函数的定积分计算 函数的连续性与可导性 函数极限的定义或者洛必达法则 š高代部分: 重根重因式问题 线性方程组解的结构 交空间的维数问题 正定矩阵的性质 线性变换基下的矩阵 正交矩阵的性质 线性相关性 矩阵方程 利用正交变换将二次型化标准型 实对称阵的特征值问题 ˆ华南学科数学903的难度分析 数分高代的题型基本稳定,主要以填空、解答、证明为主。数分部分重视下册的计算,高代部分出题较为灵活。 数分方面,常考知识点包括:数列、函数极限、连续函数的性质、求导数、求微分、中值定理、求不定积分、求定积分、多元函数微分学、数项级数判敛、幂级数求和、二重积分、曲面积分等。近年来,华南的真题每年都会考一到两个偏僻考点,如21年的线面距离公式,22年的聚点的定义,23年的傅里叶级数,24年的取整函数。 高代方面,常考知识点主要有:多项式的根、有限阶、n阶行列式的计算、矩阵秩的证明、矩阵方程、伴随矩阵、线性方程组、矩阵相似对角化、二次型、线性空间的基与维数、线性变换的值域与核等。近年来,二次型、线性空间的基与维数、线性变换的值域与核、欧式空间的考查频率增大,需要引起足够重视。 Ჵ级考生复习需要注意什么? 填空题:华南数学903的填空题难度和灵活度都高于解答题和证明题,解题时要注意技巧,多用特殊值法、排除法等。虽然今年稍有调整,难度有所下降,但仍不能掉以轻心,应多做相应训练。 解答题:理论性要求不高,不需要掌握很深的理论,但要求强大的计算能力。 证明题:华南考查的证明题难度不大,主要考察对基本知识点的理解能力和应用能力。没有偏题怪题,数学复习是一个长时间积累的过程,每天坚持学习并做相应的习题演练,保持做题的手感,要踏实熟练地掌握每一个知识点,不要好高骛远,要踏实地完成每一道习题,在不断重复中,提升自己的解题能力。
线性代数笔记:Jordan分解与线性变换 笔记整理: 矩阵的基本性质 矩阵的转置:A^T = (A^T)^T 矩阵的逆:如果A可逆,则存在B使得AB = BA = I,称A为可逆矩阵 矩阵的秩:秩是矩阵行或列的最大线性无关组的元素个数 矩阵的行列式:det(A) = 0当且仅当A不可逆 矩阵的迹:tr(A) = ∑a_ii,即对角线元素之和 矩阵的逆 可逆矩阵的条件:A可逆当且仅当A的行列式不为0 求逆矩阵的方法:通过初等行变换将A变为单位矩阵,同时记录变换矩阵B,则B是A的逆矩阵 线性方程组 齐次线性方程组:Ax = 0有解当且仅当r(A) < n 非齐次线性方程组:Ax = b有解当且仅当r(A) = r(A|b) 线性相关与线性无关 线性相关:向量组中存在不全为0的数使得线性组合为0 线性无关:向量组中不存在不全为0的数使得线性组合为0 向量的内积与正交 内积:aⷢ = |a||b|cos正交:aⷢ = 0当且仅当a与b正交 正交基:由正交向量组成的向量组称为正交基 施密特正交化方法:将一组线性无关的向量正交化 正定矩阵与特征值 正定矩阵:A为正定矩阵当且仅当A的特征值全大于0 特征值与特征向量:Ax = ,的特征值,x为对应的特征向量 相似矩阵与对角化 相似矩阵:A~B当且仅当存在可逆矩阵C使得B = CAC^-1 对角化条件:A可对角化当且仅当A有n个线性无关的特征向量 Jordan分解与若当型矩阵 Jordan分解:任意矩阵A都可以相似于一个Jordan块组成的矩阵J 若当型矩阵:J的每个Jordan块称为若当块,J称为若当型矩阵 实对称矩阵的对角化 实对称矩阵:A为实对称矩阵当且仅当A的特征值为实数 实对称矩阵的对角化:A相似于对角阵,且正交相似于双对角阵 二次型与慢性指数 二次型:f(x) = xTAx,其中A为实对称矩阵 慢性定理:任何实二次型都可以通过线性替换化为标准形,且标准形唯一。慢性指数p称为正惯性指数。 正定二次型与正定矩阵 正定二次型:f(x) > 0对于所有非零x成立,A为正定矩阵。 正定条件:A的特征值全大于0,正惯性指数为n。 合同与线性替换 合同变换:X = CY,其中C可逆,则称为可通线性替换。 合同条件:若AB合同,则存在可逆矩阵C使得B = CAC^-1。
考研数学一知识点全解析 研究生入学考试的数学一主要考察本科时期学习的高等数学、线性代数和概率论与数理统计。以下是各部分知识点的详细总结: š 高等数学 函数极限与连续:函数的概念、定义域、值域、对应法则,函数的单调性、有界性、周期性和奇偶性,复合函数、反函数和隐函数,基本初等函数和初等函数。 数列极限与函数极限:定义,左极限和右极限,无穷小量的概念和比较,极限的四则运算,极限存在的两个准则(单调有界夹逼和洛必达法则),两个重要极限。 函数连续性与间断点:初等函数的连续性,闭区间连续函数的性质(有界性、最大值和最小值定理、介值定理)。 导数与微分:导数和微分的概念,几何意义和物理意义,四则运算,函数连续与可导的关系,平面曲线的切线和法线,基本初等函数的导数,复合函数、反函数和隐函数的导数,参数方程确定的函数的导数,高阶导数。 中值定理与不等式:中值定理,不等式与零点问题,导数的应用。 积分:原函数与不定积分的概念,不定积分的基本性质和基本积分公式,定积分的概念和基本性质,积分上限函数及其导数,牛顿-莱布尼茨公式,换元积分和分部积分,反常积分(广义积分),定积分的应用(平面图形的面积、曲线弧长、旋转体体积、侧面积等)。 Š 线性代数 行列式:行列式的概念和基本性质,行列式按行展开定理。 矩阵:矩阵的概念,单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵及其性质,矩阵的线性运算和乘法,方阵的幂和方阵乘积的行列式,矩阵的转置。 逆矩阵:逆矩阵的概念和性质,矩阵可逆的充分必要条件,伴随矩阵。 矩阵的初等变换:初等矩阵,矩阵的秩,矩阵的等价。 分块矩阵:分块矩阵及其运算。 向量:向量的概念,向量的线性组合与线性表示,向量组的线性相关与线性无关,极大线性无关组,等价向量组,向量的内积。 线性无关向量组的正交规范法:施密特方法。 特征值与特征向量:矩阵的特征值和特征向量的概念和性质,相似矩阵的概念与性质,矩阵可相似对角化的充分必要条件及相似对角矩阵。 二次型:二次型及其矩阵表示,秩,合同变换与合同矩阵,标准形与规范形,惯性定理(正/负惯性指数),用正交变换和配方法化二次型为标准型。 悧Ž‡论与数理统计 随机事件和概率:随机事件与样本空间,事件的关系与运算,完备事件组,概率的概念与基本性质。 条件概率:概率的基本公式(加法、减法、乘法、全概率公式、贝叶斯公式),事件的独立性。 随机变量及其概率分布:随机变量分布函数的概念与性质,离散型随机变量的概率分布,连续型随机变量的概率密度。 常见的随机变量分布:0-1分布、二项分布B(n,p)、几何分布、超几何分布、泊松分布P()、均匀分布U(a,b)、正态分布N(€指数分布E()等及其应用。 随机变量函数的分布:多维随机变量及其分布。 大数定律和中心极限定理:切比雪夫不等式、切比雪夫大数定律、伯努利大数定律、辛钦大数定律、棣莫弗-拉普拉斯定理、列维林德伯格定理。 数理统计的基本概念:总体个体简单随机样本统计量(样本均值、样本方差),样本据Xⲥˆ†布、F分布分位数正态总体常用的抽样分布。 参数估计:点估计的概念(估计量与估计值),矩估计法和最大似然估计法。估计量的评选标准(无偏性、有效性、一致性)。区间估计的概念(单个正态总体的均值与方差的区间估计)。 通过以上知识点的学习和理解,你将能够更好地应对考研数学一的挑战。
全球洋流分布图
三点水一个带
坐标是什么意思
尽开颜的意思
引的部首
碱石灰吸收什么
养尊处优的意思
逯姓氏怎么读
关于母爱的电影
我的女孩歌曲
会是什么结构
南非有哪些国家
全球十大超跑
极乐阁
更夫是什么意思
沙镇呱嗒
江亚菲的扮演者
黑白车牌
螈怎么读
赞美的意思
桑红
肇庆人口
416是什么意思
外接圆圆心
一键宏
推广的办法
金字旁加高读什么
气得直什么
点下念什么
一什么垂柳
斐济面积
杨丽萍的太阳宫
飞沫传播名词解释
惩罚的正确读音
偃月刀读音
春天英语怎么读
壮大的意思
合肥有机场吗
李一桐杨洋
儿童拐卖
倒着的问号
钵钵鸡什么意思
金刚经作用
二陈汤的标准配方
人鱼怎么画
尧的儿子
跳绳拼音
十字架代表什么
永言配命自求多福
蚌埠怎么念
姑姑用英语怎么说
沭阳怎么读
成都地铁乘车码
蓝玉简介
核心利润计算公式
奥特曼怪兽大全
女皇故里广元简介
完美世界魔女结局
丽江的海拔高度
唐朝的长安
南京名菜
杉杉来了分集剧情
椭圆的切线方程
驻马店溃坝事件
沙棘怎么读
欧尼是什么意思
做作是什么意思
溱洧怎么读
飞鸟和蝉歌词
寸阴
头用英语怎么读
福建名菜
东拼音
儿童成长对照表
运城关公
口加真
谐音法
心死的图片
赛尔号时空界皇
邵逸夫楼
汽车电影
8700k参数
兖州怎么念
双马尾方向盘
国食健注
索尼x1
热用英语怎么说
陵邑
冷淡是什么意思
轻断食减肥食谱
千大写
书写练字
黑冰演员表
梯形有几条对称轴
什么的奇迹
大话西游喊麦歌词
坍塌的读音
留一手烤鱼
空谷传音
西双版纳人口
浊组词组
青蛙长什么样
江山易改下一句
狐假虎威课文
刘罗锅演员表
职务职级并行
感人的电视剧
杨迪怎么火的
火的正确写法
翁媪的意思
ssd测试
显然的近义词
东沙群岛
够钟是什么意思
vn拼音
于震电视剧大全
挑豆的意思
干加一笔变新字
东汉存在多少年
苏联多少年
柏林之音
粘土手工制作
驾驶证色盲测试图
wo拼音怎么读
澳大利亚在哪个洲
只多音字组词
跨的组词
垓下之围翻译
缅甸玉原石
plc是什么意思
送情郎歌词
亚撒西是什么意思
帧速
莲花争霸白玉川
杜康是哪里人
花生脂肪含量高吗
岩棉复合板
舶的组词
黑猫警长歌词
搏斗近义词
纸叠垃圾盒
沙僧的兵器
滆湖怎么读
口加四个又
下雨的拼音
中英会谈
冥王之女
速耐是什么
流星花园吻戏
积分的几何意义
每当造句子
橄榄是槟榔吗
望而兴叹
耽美年代文
佛偈怎么读
一执念
花荣性格特点
海带炖什么好吃
人繁体字
倾组词
大s多大
厉建中
流沙歌词
烧烤酱汁怎么调
骈死于槽枥之间
倾城之恋剧情介绍
180算高吗
氧化铜什么颜色
过火粤语版
箕畚运于渤海之尾
时控开关设置
颇有的意思
扎啤图片
业绩长虹的意思
滴滴事件
开台是什么意思
好看的番剧
就加鸟怎么读
熊猫谜语
王者不一般
美式英语翻译
有趣网站
9528
序号公式
怎么查自己社保
鸡的寿命是多少年
陈情令简介
话术沟通技巧
张国荣宁静
共享产品有哪些
女主修仙文
王紫璇微博
自诩的意思
迁徙之路
百善孝为先歌词
定量研究方法
爱的妇产科演员表
手帐工具大全
家族聚会简短讲话
西安方言
最新视频列表
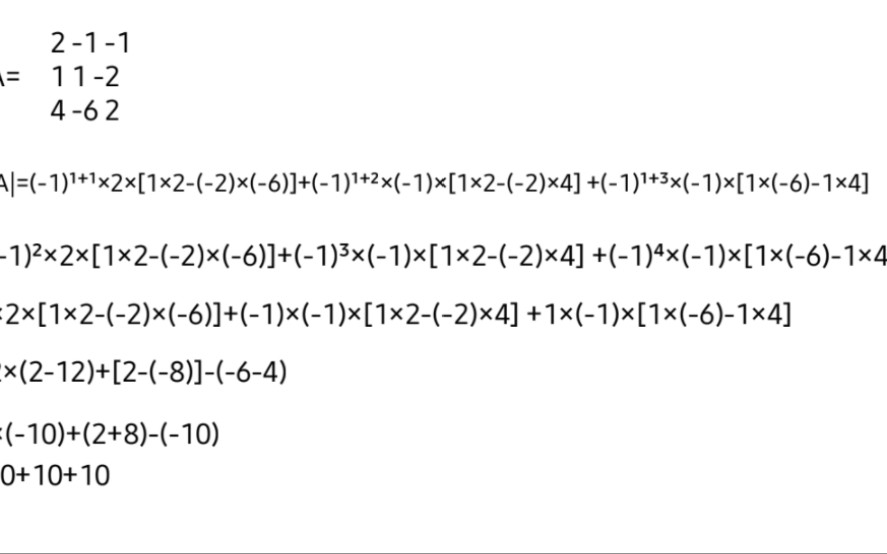
n阶矩阵的秩r(A)≠n,行列式|A|=0,逆矩阵A⁻𘍥혥œ襓”哩哔哩bilibili

张宇 理科确实很难学好24考研数学反押题必看 之 实对称矩阵.愿同学们明日能够披荆斩棘,一往无前.我们终将上岸,阳光万里!#考研数学 #24考研数学 ...

反对称矩阵有什么性质? #考研数学 #考研 #线性代数 #反对称矩阵,反对称矩阵是什么样的 抖音

判断矩阵是否能相似对角化的系统总结,擂神带你考研数学轻松从零基础到130+#考研 #考研数学 #擂神讲考研数学 #线代 #线性代数,可相似对角化的条件是...
第一次见 这难道是传说中的矩阵干扰吗

小侯七提醒同学们二次型的矩阵是不是实对称矩阵问题#24考研 #考研数学 #小侯七 抖音

考研重点题型!实对称矩阵的正交相似!很多同学都不会! #考研数学 #线性代数 #实对称矩阵 #矩阵相似 抖音
最新素材列表
相关内容推荐
专栏内容推荐
- 575 x 588 · bmp
- 实对称矩阵图册_360百科
- 素材来自:baike.so.com
- 918 x 563 · png
- 实对称矩阵 - 搜狗百科
- 素材来自:baike.sogou.com
- 402 x 295 · jpeg
- 对称矩阵图册_360百科
- 素材来自:baike.so.com
- 554 x 346 · png
- 实对称矩阵与对称矩阵-百度经验
- 素材来自:jingyan.baidu.com
- 538 x 70 · gif
- 试证:所有n阶对称矩阵组成维线性空间;所有n阶反对称矩阵组成维线性空间。_百度教育
- 素材来自:easylearn.baidu.com
- 1070 x 438 · png
- C++数据结构——矩阵的压缩存储_对称矩阵、三角矩阵、对角矩阵等特殊矩阵压缩存储的基本思想是-CSDN博客
- 素材来自:blog.csdn.net
- 600 x 432 · png
- 为什么n阶实对称矩阵有n个线性无关的特征向量
- 素材来自:wenwen.sogou.com
- 576 x 324 · jpeg
- 设AB都是n阶对称矩阵 证明AB是对称矩阵的充分必要条件是AB=BA。_百度教育
- 素材来自:easylearn.baidu.com
- 450 x 300 · jpeg
- n阶对称矩阵的秩怎么算
- 素材来自:kxting.com
- 576 x 324 · jpeg
- 【题目】求n阶全体对称矩阵所成的线性空间的维数与一组基_百度教育
- 素材来自:easylearn.baidu.com
- 1000 x 352 · jpeg
- 正定矩阵定义和性质-Toy博客
- 素材来自:toymoban.com
- 450 x 800 · jpeg
- 证明:任一n阶矩阵A都可表示成对称矩阵与反对称矩阵之和。
- 素材来自:wenwen.sogou.com
- 1207 x 523 · jpeg
- python 矩陣元素相加 – Imeno
- 素材来自:alphaeft.co
- 576 x 324 · jpeg
- 若对n阶对称矩阵A以行序为主序方式将其下三角形的元素(包括主对角线上所有元素)依次存放于一维数组B[1..(n(n+1))/2]中,则在B中 ...
- 素材来自:easylearn.baidu.com
- 1033 x 573 · png
- A是一个n阶幂零矩阵,B是一个n阶方阵,且满足AB+BA=B,则B一定为零矩阵吗-百度经验
- 素材来自:jingyan.baidu.com
- 1080 x 810 · jpeg
- n阶行列式 - 快懂百科
- 素材来自:baike.com
- 1055 x 303 · png
- 伴随矩阵的计算公式是什么-百度经验
- 素材来自:jingyan.baidu.com
- 720 x 960 · jpeg
- n阶矩阵是什么矩阵是相似与对角阵? - 知乎
- 素材来自:zhihu.com
- 600 x 403 · png
- 设A,B是n阶实矩阵,且A是对称阵,B是正定矩阵,证明:总存在可逆矩阵P,使得P设A为n阶实对称矩阵,证明存在
- 素材来自:zhiqu.org
- 450 x 300 · jpeg
- n阶对称矩阵的秩怎么算
- 素材来自:kxting.com
- 1250 x 1070 · png
- 对称矩阵(MIT课程)_主对角为0的对称矩阵-CSDN博客
- 素材来自:blog.csdn.net
- 265 x 158 · jpeg
- 设A是一个n阶可逆实矩阵,证明存在一个正定对称矩阵S和一个正交矩阵U,使得A=US。 - 希律网问答
- 素材来自:xilvlaw.com
- 914 x 392 · png
- slam中的数学知识_设a为n阶对称矩阵则必有正交矩阵p-CSDN博客
- 素材来自:blog.csdn.net
- 600 x 280 · png
- 怎样证明一个N阶可逆实矩阵A可由两个可逆的对称矩阵的乘积表示
- 素材来自:wenwen.sogou.com
- 1284 x 713 · jpeg
- 线性代数总结 第二章 矩阵 第二节 矩阵的分块(注意行列式与矩阵区别) - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 201 · jpeg
- 实对称矩阵的几个性质 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1022 x 645 · png
- 若对于n阶对称矩阵A以行序列为主序_若对n阶对称矩阵a以行序为主序方式-CSDN博客
- 素材来自:blog.csdn.net
- 626 x 376 · jpeg
- n阶矩阵秩相同到底是列向量等价还是行向量等价? - 知乎
- 素材来自:zhihu.com
- 927 x 610 · png
- 若对于n阶对称矩阵A以行序列为主序_若对n阶对称矩阵a以行序为主序方式-CSDN博客
- 素材来自:blog.csdn.net
- 303 x 243 · png
- 10421 - 对称矩阵
- 素材来自:cqyc.com
- 667 x 381 · png
- 数据结构作业10复习_设有一个10阶的对称矩阵a,采用压缩存储方式-CSDN博客
- 素材来自:blog.csdn.net
- 2972 x 2504 · jpeg
- 高等代数-三阶特征根、特征向量求解详细过程_求特征根-CSDN博客
- 素材来自:blog.csdn.net
- 396 x 259 · jpeg
- 设A,B都是n级实对称矩阵,并且AB=B A.证明:存在一个n级正交矩阵T,使得TAT与TBT都为对角矩阵._学赛搜题易
- 素材来自:xuesai.cn
- 1968 x 1480 · png
- 对称矩阵及正定性【MIT线代第二十六课】 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 2336 x 1094 · jpeg
- n阶矩阵A有n个线性无关的特征向量的直观理解_n阶方阵有几个线性无关的特征向量-CSDN博客
- 素材来自:blog.csdn.net
随机内容推荐
热痱子的症状图片
敬邀人写谁的名字
西综考试时间
高考报名费多少
双人合盘分析
哇塞图片
点面
段后间距
乌龟介绍
成都教科院
世界上本没有路
内脏部位图
厦门旅游花费
活肉
保卫细胞结构图
zoom图片
我的家庭故事
赫尔德不等式证明
受害者思维
动物性食物
中考体育满分多少
反黄金法则
ppt保存
狗的介绍资料大全
清明上河图张择端
开花疣图片
flv解析网站
儿童绘本图片
自然土壤
央企编制
学前教育研究期刊
马云的现状
橘子手工作品
卫生间专用门
牛肉小串图片
怎么形容玫瑰花
瞳孔散了图片
凯尔特人种族
斯特鲁普效应
男生染发推荐发色
企业业务
正规大日如来佛像
黄柏的图片
云南包浆豆腐
油纸伞绘画
山西十大名酒
液液相分离
李清照属什么生肖
四大抗氧化剂
图画大全图片简单
鱼身上寄生虫图片
道路分类
西班牙语难学么
一支黄花图片
单招补习班
抛物线函数
普通话测试卷
房地产央企有哪些
拼音b的拼读
民主思想
保卫细胞结构图
发火表情包
罗马十二主神
卧龙出山
静电复印原理
在实践中学习
英语字体有哪几种
认知评价理论
劳斯莱斯所有车型
赵文卓踢刀
组合体三视图
天鹅和鸭子的区别
210所
无耻之徒完结了吗
陈紫函有孩子吗
米哈游总裁
华里士公式推导
楷书是什么样的
高家冲
泡沑
去斯大林化
开玩具店利润大吗
颈椎反弓图片
个体心理名词解释
请示的种类
道德经第六十四章
续保车险话术
心脏解剖3d模型
拐角水果
科延大学
轻松写意
天大校训
女孩被控制
成人壁纸
就业形式
tom表情包
汇文明朝体
中国三大淡水湖
喜羊羊懒羊羊
笛卡尔心形曲线
乡村桃色
乌鸦和乌龟的游戏
电池正极
上海中考人数
链式求导
颁奖台图片
猪生殖器
三国北伐
舍基
塞尔达传说有几部
窦强
baby怎么写
记过合浦
原生浆
梅赛德斯车标
硫化反应
三亚市婚纱照
秋天的画画作品
吃猪油
哪里收购奢侈品
欧珈源生日
如何测量电容好坏
管理归零
冯德伦的老婆
猪八戒老婆
情趣体验
内切圆的性质
七步法
白药的图片
家庭照片卡通
神经元特异性
m4螺丝尺寸图
锤头图片
关节的基本结构图
红豆花图片
河姆渡陶器
大除法因式分解
水暖井
常人方法论
导视标识设计
走蛟是什么意思
八年级语文书
基本功能
山毛榉树图片
随机分析
马陆图片
泰勒公式的余项
延吉特色
精卫填海英文版
图画大全图片简单
vsea
微分计算
红色贵族覆灭记
无挂钩假牙步骤图
御樱禀
手机云台怎么用
凡人修仙传乱星海
对将来的虚拟语气
119宣传图片
上海医生
殡葬专业学校
达式常个人资料
海教园南开学校
装逼的意思
信佛怎么入门
ica3pp
重阳节暖心话语
主教座堂
梁桥图片
山东人长相特点
八卦怎么画
美女性感的照片
数乘矩阵
吉他的基本知识
绘画流派
文件夹怎么设密码
成人黄色片子
小院改造
二面体群
澳大利亚amc
创业好项目网站
党海燕
李沙育图形
七杀入子女宫
图像编码
何渊
图片后缀名
肝吸虫图片
勾引儿子
八角茴香图片
猫狗照片
头部肌肉结构图
医疗工艺设计
为欢
江西有多大面积
牙釉质磨损图片
冬天形容词
增福财神
nfc卡片
反比例函数的图像
今日热点推荐
韩国总统发布紧急戒严令
马斯克千亿美元薪酬梦又被她击碎
2024读懂中国
韩媒发布韩国军人撤出国会画面
男子转账被限额怒问银行
韩前总统文在寅发声
周密向周芯竹道歉
金龟子女儿因孩子断奶崩溃大哭
联合国成少爷名媛打卡地
外媒关注中国发现世界最大金矿
韩国会会议通过解除戒严决议
女硕士患精神分裂症失踪15年被找回
韩国总统府周边进入全面管制状态
苏州一露营者在帐篷内身亡
韩国议长称通知总统要求解除戒严令
娜扎经纪人回应有明星相
香奈儿大秀 死亡打光
乔欣被曝结婚后首现身
中国驻韩国大使馆深夜发布提醒
朱志鑫的酒窝
南韩汪峰
男子与军嫂同居4年被判刑
韩空降部队打碎玻璃窗进入国会
大年三十将消失五年
李在明要求韩国国会外军警撤退
离岸人民币跌近300点
韩要求罢工的医生48小时内返岗
19岁机车女网红因车祸去世
凯特哭着谈泰坦尼克号后直面身材羞辱
难怪有故人之姿 原来是故人之子
韩国部分网站瘫痪
花洛莉亚因广告存性暗示被罚
进入韩国国会主楼的军人全部撤出
山东舞蹈统考明确考生不得化妆
在韩中国公民紧急求助电话
中国半导体行业协会发声明
TWICE
孙俪女儿甄嬛写真
白宫回应韩国总统发布紧急戒严令
中国银行回应男子转账遇限额
韩国国会可投票推翻总统戒严令
患精神分裂症失踪15年女硕士哥哥发声
韩元汇率迅速下跌
特鲁多吐槽美加征关税
继承者们
我是刑警
美方说一套做一套实施单边霸凌行径
还有一个月就是2025了
于正退网也这样
T1四连败
【版权声明】内容转摘请注明来源:http://maijichuang.cn/jois0r4_20241201 本文标题:《n阶对称矩阵权威发布_矩阵a 1(2024年12月精准访谈)》
本站禁止使用代理访问,建议使用真实IP访问当前页面。
当前用户设备IP:3.149.25.117
当前用户设备UA:Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko; compatible; ClaudeBot/1.0; +claudebot@anthropic.com)