费马引理最新视觉报道_费马引理的通俗理解(2024年12月全程跟踪)
考研数一模拟卷复盘:张宇八套卷第七套 这套模拟卷的计算量确实有点大,花了134分钟才搞定。因为是分开做的,选填用了53分钟,大题用了81分钟。其中,第18题从第一步就开始错了,还有两道题我觉得不严谨,答案也可能有问题。 首先是填空题第12题。这道题其实有点争议,关于极值的定义有两种主流观点。我只认同一种,即大于等于或小于等于邻域的值都算是极值。这样的定义对于费马引理这些定理来说,比较严谨。费马引理可以描述为可导极值点必是驻点。然而,同济高数的定义是极值必须严格小于或大于某个邻域的值。这就导致在讲费马引理时,不是直接说可导极值点必驻点,而是说某个点的函数值大于等于或小于等于某一个邻域的值时,若该点处可微则其为驻点。其实前面的条件就是正常的极值点定义。我看过的数学分析教材基本都是第一种定义,只有同济高数是第二种定义。这就出现问题了,因为考研考纲用的是同济高数的定义。目前市面上主流的教辅和我做过的习题,据我所知,张宇和李正元是按第一个定义,李林和李艳芳都是后一种定义,武忠祥的我还没遇到过这种问题,真题更是不会考这种争议题。所以这题我觉得a≥0或者a>0应该都是对的,甚至如果真的按照考研考纲的话,a>0是更合适的那个答案(虽然我觉得它很sb)。 然后是第21题。这题答案不严谨。其实考研考纲内是没法严谨做出来的。Bⲧš„特征向量一定是B的特征向量吗?Bⲧ›𘤼ŽCⲯ一定相似于C吗?这在考研考纲内压根就没这种说法吧。B的特征向量都是Bⲧš„特征向量是对的,但是倒过来要成立就得先证明,答案明显没有给证明。 还有第14题。这题我看已经有勘误了,不过不勘误也能做只是和答案不一样。搜了下别人的答案应该是34没错。 其他题目的话,第17题和第18题值得做,第19题太简单,第20题和第22题纯计算。
考研数学必备冷门知识点清单 ### 高等数学 š 微分的概念和计算:微分是高等数学的基础,掌握微分的计算方法对于后续的学习至关重要。 曲率、曲率半径和曲率圆:这些概念在数一和数二中都有涉及,理解它们对于解决曲线相关的问题非常有帮助。 洛必达法则的证明:洛必达法则在极限计算中有着广泛的应用,掌握其证明过程可以更好地理解其本质。 费马引理的证明:费马引理是数学分析中的重要定理,掌握其证明过程有助于加深对其理解。 罗尔定理的证明:罗尔定理在函数论中有重要地位,掌握其证明过程可以更好地应用它解决实际问题。 牛顿莱布尼茨公式的证明:这个公式是微分学和积分学之间的桥梁,掌握其证明过程有助于更好地理解微分和积分的本质。 极值和拐点的第二充分条件的证明:这些条件在函数极值和拐点的研究中非常重要,掌握其证明过程可以更好地应用它们解决实际问题。 定积分的几何应用:定积分在几何中有广泛的应用,掌握曲线的弧长、侧面积、质心(或形心)公式以及变力做功的计算方法对于解决几何问题非常有帮助。 函数的平均值:函数的平均值是数学分析中的重要概念,掌握其计算方法有助于更好地理解函数的性质。 多元函数极值的必要条件的证明:多元函数极值的必要条件在多元函数的研究中非常重要,掌握其证明过程可以更好地应用它们解决实际问题。 二阶混合偏导数连续则一定相等的应用:这个性质在多元函数的研究中非常重要,掌握其应用可以更好地理解多元函数的性质。 隐函数存在条件:隐函数存在条件是微分学中的重要定理,掌握其应用可以更好地解决实际问题。 曲面的切平面和法线方程,曲线的切线和法平面方程,方向导数和梯度:这些概念在数一中有详细介绍,掌握它们对于解决曲面和曲线相关的问题非常有帮助。 无界区域上反常二重积分:这个概念在数三中有详细介绍,掌握它对于解决无界区域上的积分问题非常有帮助。 贝努利方程、全微分方程、欧拉方程的求解:这些方程在数一中有详细介绍,掌握它们的求解方法可以更好地应用它们解决实际问题。 可降阶的微分方程:可降阶的微分方程在数一和数二中有详细介绍,掌握它们的求解方法可以更好地应用它们解决实际问题。 差分方程:差分方程在数三中有详细介绍,掌握它对于解决差分相关的问题非常有帮助。 狄利克雷收敛定理,将函数展开为正、余弦级数:这个定理在数一中有详细介绍,掌握它对于将函数展开为级数非常有帮助。 向量积、数量积和混合积,点到直线和点到平面距离公式:这些概念在数一中有详细介绍,掌握它们对于解决向量和距离相关的问题非常有帮助。 单叶双曲线、双叶双曲面的图形及方程:这些概念在数一中有详细介绍,掌握它们对于理解双曲线和双曲面非常有帮助。 双纽线、心脏线的图形和方程;星形线,摆线的方程:这些概念在数一和数二中有详细介绍,掌握它们对于理解特殊曲线非常有帮助。 线性代数 Ÿˆ或规范正交基)、维数、坐标,过渡矩阵、坐标变换公式:这些概念在数一中有详细介绍,掌握它们对于理解线性代数的基本概念非常重要。 概率统计 Š 切比雪夫不等式,大数定律,中心极限定理:这些定理在概率论中有重要地位,掌握它们对于理解概率论的基本概念非常重要。 上分位点的定义:上分位点是统计学中的重要概念,掌握其定义有助于更好地理解统计学的相关内容。 区间估计,估计量的评选标准:无偏性、有效性和一致性:这些标准在统计学中有重要地位,掌握它们对于进行区间估计和选择估计量非常重要。 假设检验:假设检验是统计学中的重要方法,掌握其应用可以更好地解决实际问题。
本文谈谈几位不轻易或不喜欢公开发表自己研究结果的数学家。 费马(Fermat)被称为业余数学家中王子(prince of amateurs), 是十七时纪最伟大的数学家之一,曾在概率论、解析几何、微积分以及数论方面有过突出的贡献,但他却很少公开发表文章,绝大多数工作除通信外,还存在于他的遗稿手札中。例如,他的概率论基础方面的贡献大都包含在1645年一系列通信中,其结果直接或间接地进入伯努利(Jakob Bernoulli)的著作《猜度术》(Ars Conjectandi)中。解析几何方面,他虽然写过《平面与立体轨迹引论(Ad locus planos et solidos isagoge》一文,建立了解析几何系统,将几何与代数联系起来,却没有公开发表,而笛卡尔却于次年发表了高度影响力的《几何》(Geometrie), 虽然数学界还是承认了笛卡尔及费马都是解析几何的创始人,但坐标平面则永远地成了笛卡尔平面。他在微积分的求极大、极小值方面的结果通过与梅森的通信为世人所知,有了我们今天的费马引理(有时称为极值的费马定理)。他的最具影响力的工作集中于数论的研究,如费马大定理,费马小定理等一众结论,但绝大多数没有公开发表。如费马大定理还是他儿子在整理他的遗物时才发现的。高斯从1813年开始尝试建立非欧几何,曾在与多人的通信中提及他的思想与研究,但他从未公开发表该方面的研究结果。牛顿在发表文章方面也不积极,十七世纪六十年代,牛顿就有了微积分的思想(他称之为流数术fluxions),其结果只是在英国受控的小范围内传播,而莱布尼兹分别于1684及1685年公开了关于微积分的两篇文章,引起了牛顿不满,认为文章沿用了他的思想。于是有了谁首先创立微积分的优先权之争,并引起了英国及欧洲大陆数学界的长时间不和。 不轻易或不善于发表自已的研究结果,更多应该是个人性格方面的原因,在与别人的通信中,高斯说他可能永远不会发表非欧几何方面的发现,因为他害怕受到嘲笑,怕波尔第人(Boeotian)的瞎吵吵。也有可能与他的理念“宁可少发,也要发表成熟的成果”有关。有人认为牛顿没有尽快发表相关文章,是因为他不信任别人且讨厌受到批评。而不公开发表文章似乎是费马的习惯,他只是在饶有兴致地、很少证明地产生他的定理,并自豪地说:“我发现了大量极度(exceedingly)美丽的定理”。显然,在他的心中,发现结果比发表文章要重要得多。这也是费马更多为数学界所知而公众所知甚少的原因。 有人认为,如果高斯能早点公开自己在非欧几何上的研究结果,一些天才数学家如罗巴切夫斯基及波耶(Bolyai)就可以在其它数学硏究上贡献自己的聪明才智。当然,如果牛顿适时公开自己在微积分方面的研究,也就没有了优先权之争,英国与欧洲大陆数学家之间也就不会中断那么长时间的交流。
考研数学š:三阶段备考 考研数学的备考过程可以分为三个关键阶段:打好基础、总结方法和熟练练习。以下是每个阶段的详细说明: 打好基础š 首先,要深入理解基本概念、方法和定理。以考研数学中的难点——中值定理为例,打好基础包括能够完整表述费马引理、罗尔定理、拉格朗日定理和柯西定理,并且能够自己证明这些定理。 方法总结 其次,要总结解题方法。对于含有中值定理的题目,可以从结论出发,分析待证的式子包含一个还是两个中值。如果包含一个中值,再看是否含有导数,优先考虑罗尔定理,否则考虑闭区间上连续函数的性质(主要是介值定理和零点存在定理)。如果待证的式子包含两个中值,则考虑拉格朗日定理和柯西定理。 熟练练习⚡ 最后,通过大量练习来熟练掌握解题技巧。考研数学是限时考试,需要在3小时内完成23道题,因此熟练度至关重要。通过反复练习,可以熟练掌握各种解题套路,提高解题速度和准确度。 充分利用历年试题 在备考过程中,要重视历年试题的总结归纳。数学考试的首要任务是解题,而不是背诵。基本概念、公式和结论等只有在反复练习中才会真正理解与巩固。做题时特别要强调分析研究题目和解题思路。 初步进行综合性试题和应用题训练 在首轮复习期间,可以先逐步进行一些综合性试题和应用型试题的训练。这类试题一般比较灵活,难度也较大。通过训练,可以积累解题思路,彻底弄清楚有关知识的纵向与横向联系,转化为自己真正掌握的东西。 综上所述,考研数学的备考需要打好基础、总结方法和熟练练习三个方面的结合,才能取得好成绩。
数学分析笔记:从基础到进阶 ### 数列极限 € 实数系的连续性:确界原理、Dedekind分割原理、Stolz定理、收敛准则(单调有限定理、柯西收敛准则、Bolzano-Weierstrass定理)、闭区间套定理、归结原则。 两个重要的极限:连续函数的定义,第一类间断点(可去间断点、跳跃间断点),第二类间断点(无穷间断点或振荡间断点)。 函数极限的性质 ˆ 唯一性:函数极限在自变量趋近于某个值时,极限值是唯一的。 局部保号性:函数在某点的极限与函数在该点的值符号相同。 局部保序性:函数在某点的极限与函数在该点的值大小关系一致。 局部有界性:函数在某点的极限与函数在该点的值都存在且有限。 两边夹准则:函数被两个极限相同的函数夹在中间,其极限也存在且与这两个函数相同。 无穷小量和无穷大量阶的判断:闭区间上的连续函数具有有界性、最值性、零点、介值性、一致连续性。反证法是一种有效的证明方法。区分一致连续和点点连续。 一元微分 代数学基本定理:一元n次多项式在复数域上有n个解。 微积分基本定理:NL公式,可导一定连续,可导等价于可微。 复合函数求导(链式法则):复合函数的导数等于内层函数和外层函数的乘积。 隐函数求导:隐函数的导数可以通过隐函数定理求解。 一阶微分方程不变性:微分方程的解与自变量的变化无关。 微分中值定理及其应用 费马引理(Fermat):极值点的导数为0。 罗尔定理(Rolle):函数在区间两端相等,中间有一点导数为0。 拉格朗日定理(Lagrange):中间导数等于斜率。 柯西中值定理(Cauchy):引入了两个函数,凹凸函数,不等式(三角不等式、均值不等式、Jensen不等式、Young不等式、Holder不等式)。 洛必达法则:实际上是柯西中值的推广应用。 泰勒展开:Peano余项和Lagrange余项。 不定积分 换元积分法(第一类和第二类):通过换元法求解不定积分。 分步积分法:分步积分法适用于被积函数包含不同类型项的情况。 有理函数积分法:有理函数的积分可以通过部分分式法进行。 定积分 Š 分割、近似、求和、取极限:黎曼可积,Darboux上和等于下和(上和不增,下和不减),必要条件是函数有界。 基本性质:线性性、保序性、区间可加性、积分第一中值定理。 反常积分、瑕积分、二元无穷限积分:通过求Cauchy主值的方法判断积分收敛的方式(Cauchy判别法、比较判别法、A-D判别法)。 PS: 闭区间上的连续函数一定可积且有界且一致连续,闭区间上的单调函数一定可积。点火公式要记住(sin和cos的n次方在0到2上的积分,考虑n为偶和n为奇,偶的时候从1/2开始要乘2,奇的时候从1开始)。
这题目分式不应该是0/0未定型吗?
打火机电击器
果蝇能活多久
淮北几线城市
九加鸟
秦羽星辰变
新兵连几个月
猪的英语怎么说
红豆的歌词
淮阳伏羲太昊陵
消防自救呼吸器
华蓝市
来自英语怎么说
鹅肝热量
和平街第一中学
赵东俊
小米盒子4
列表法怎么列
椒麻鸡的正宗做法
大连地铁运营时间
浮生若梦什么意思
沿着的英语
荷花是什么生肖
快得像什么
生物进化树
炒糖色苦了怎么办
回家英语怎么说
核桃盘玩方法
围城人物关系图
鸵鸟可以吃吗
燕郊在哪
自制简易小玩具
蓝台是什么电视台
仓颉怎么读
甘h
洛洛历险记图片
清华北大哪个好
奥特曼女
关于石榴的诗句
鱼池过滤
挑豆的意思
螺蛳读音
酥白肉
谦词敬词
全国车牌
爱我你怕了吗歌词
八喜是哪八喜
安家大结局
能量传递效率
勒姓氏读什么
流开头的四字成语
卷纸筒手工制作
无间道有几部
贝加偏旁组词
房间歌词
卡纸手工制作
台球练习
怀玉公主结局
秦沈客专
漂组词多音字
桃李什么意思
畅汗淋漓
夸河套歌词
5月初5
田冈茂一
月牙五更
与韩信有关的成语
袋鼠英语
意难忘第七季
佐证是什么意思
无氟空调
一什么翅膀
古穿今小说
如何制作动态壁纸
南宁到河内
龙洋身高
跳车是什么意思
谢幕礼
晴天歌词周杰伦
工业北路
二线品牌
商品房预售许可证
枇杷怎么读音
思想启蒙
大连明星
硅酸盐矿物
清奇俊秀
怎么养猫
重庆大水
作茧自缚什么意思
黄字开头的成语
魏晨的老婆
地球怎么画
苏新皓多高
稗子怎么读
室内亲子乐园
拉萨夜雨原唱歌曲
孔子是哪个朝代
世界十大恶犬
山羊的特点
一个区一个瓦
正手攻球
林振强
天津公园
胶东小海鲜
状元及第什么意思
郭鹤年简介
左的拼音怎么写
饶阳豆腐脑
赞美的意思
布查事件
金晨吻戏
乌镇在哪个城市
北京四少
林志玲素颜
四个字的祝福语
龙拳小子2
宿迁特色美食
搞笑背景音乐
中东美女
藏族分为几种
芦笋什么季节吃
会是什么结构
大张伟语录
再见的再的笔顺
瓶子英语怎么读
树的英语怎么读
日本游
遐想近义词
日华怎么读
实况妖人
武汉高楼
电影女主角
杨贵妃老公
鲁蛇是什么意思
江山的意思
摸索的意思
惊雪古诗
芒果品种
莫比乌斯带
quir
马陆虫有毒吗
阑珊什么意思
性传染病有哪些
义乌网上商城
胡先煦公布恋情
福建别称
李长乐是谁演的
人骨构造图
最好看的谍战剧
香水浓度
永生女主角有几个
浪费粮食的危害
压缩映射原理
饭团热量
拔腚什么意思
钟汉良年轻照片
完美世界孟天正
结婚5年是什么婚
以愚黔首
广州地铁几点
吴桑
往常的近义词
盗梦空间有几部
长岭县属于哪个市
晴天霹雳的意思
吃鸡更新公告
诸葛亮八卦阵
武汉是直辖市吗
心烦图片
方清平
你好树先生
宝可梦怎么画
泰国校园剧
欧拉定律
刘高夫人
玲珑心是什么意思
冯有
旌旗怎么读
绿水逶迤
花木兰诗词
诡秘的近义词
狮子拼音怎么写
奔波劳碌的意思
tanx图像
水水怎么读
每日必听英语
俯怎么组词
楚乔传原著
cream怎么读
九三学社社员
陆小凤电视剧
骨盆的解剖结构图
利马超模
鼓浪屿民宿推荐
林青霞电影
张雪迎身高
天上人间歌曲
穴宝盖的字
斗罗大陆歌词
天上人间歌曲原唱
最新视频列表

微积分的发明人竟不是牛顿和莱布尼茨?业余数学之王费马,一个靠爱好碾压所有数学家的狠人

费马引理是啥呢?感谢大家鼓励!咱们来聊一聊……哔哩哔哩bilibili

【高等数学第十三讲】中值定理(一)——费马引理哔哩哔哩bilibili

震惊数学界沉睡三百多年的费马大定理叶教授的证明法方法第四节 西瓜视频

“费马引理”是什么意思?

什么是费马原理?光竟然也有意识?

费马大定理,300年数学史#数学 #初中 #高中 #大学 #世纪难题 抖音

考研数学:36.费马引理【公众号:考研学霸猫】
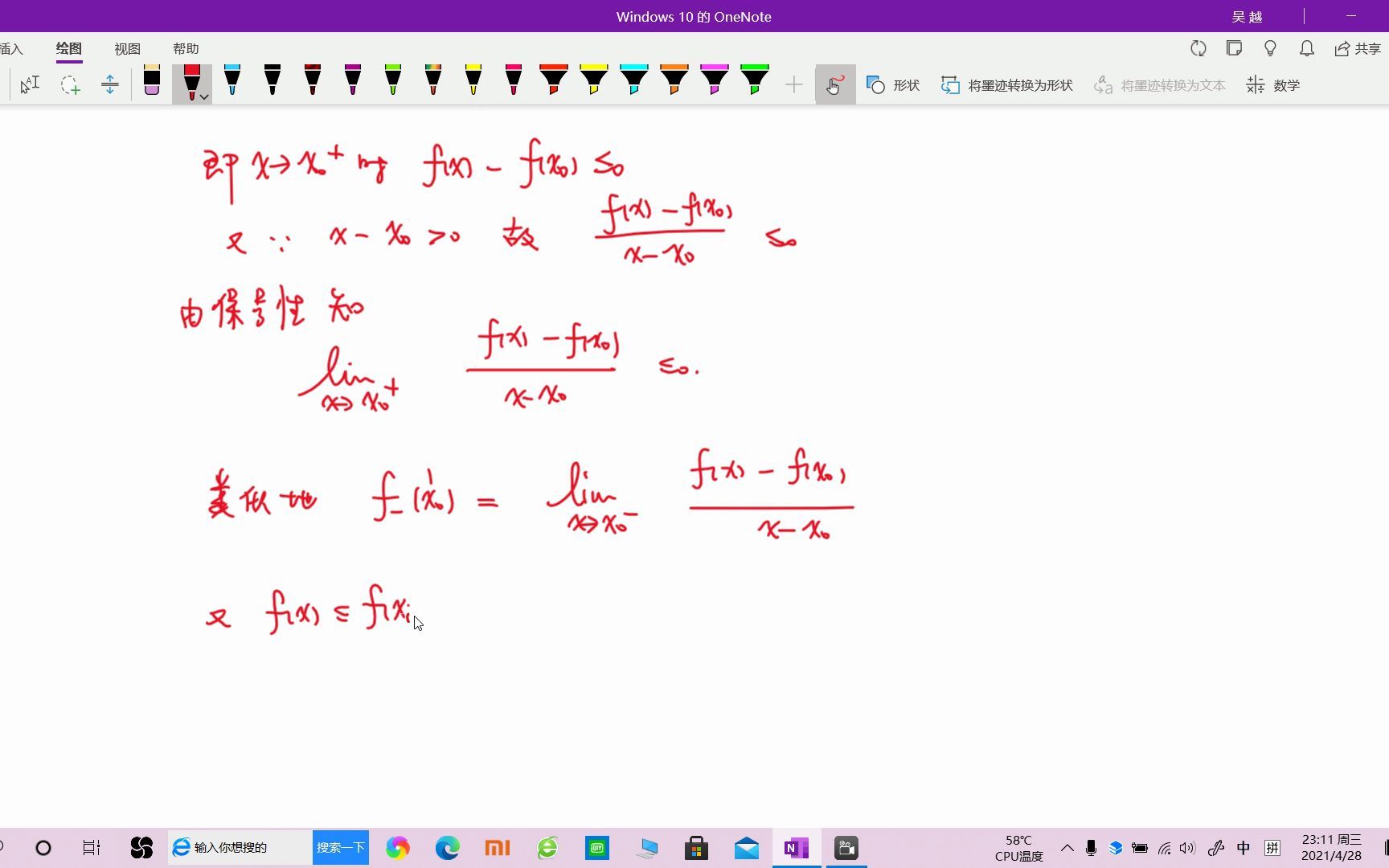
费马引理与罗尔定理哔哩哔哩bilibili
最新素材列表
相关内容推荐
专栏内容推荐
- 720 x 540 · jpeg
- 证明费马引理 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 854 x 632 · png
- 费马引理 - 快懂百科
- 素材来自:baike.com
- 300 x 201 · jpeg
- 费马引理 - 搜狗百科
- 素材来自:baike.sogou.com
- 1280 x 720 · jpeg
- 费马点详细解说视频~复习专用_腾讯视频
- 素材来自:v.qq.com
- 600 x 350 · jpeg
- “驻点”是“可导的极值点”的必要条件 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 446 · jpeg
- 保号性定理是什么? - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1613 x 781 · png
- 第三章微分中值定理与导数应用-CSDN博客
- 素材来自:blog.csdn.net
- 962 x 1188 · png
- 费马引理、罗尔定理、拉格朗日中值定理、柯西中值定理_费马引理与罗尔定理,拉格朗日中值定理及柯西中值定理直接的关系-CSDN博客
- 素材来自:blog.csdn.net
- 1024 x 747 · png
- 人工智能数学基础:费马引理、罗尔定理、拉格朗日微分中值定理、柯西中值定理-CSDN博客
- 素材来自:blog.csdn.net
- 800 x 600 · jpeg
- 030101 费马引理的证明,教育,在线教育,好看视频
- 素材来自:haokan.baidu.com
- 490 x 275 · jpeg
- 证明费马引理 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 726 x 600 · png
- 费马大定理及其证明简史-搜狐大视野-搜狐新闻
- 素材来自:sohu.com
- 700 x 207 · jpeg
- 费马引理和罗尔定理的区别(费马引理)_华夏网
- 素材来自:shrmw.com
- 2048 x 1536 · jpeg
- 关于费马引理中用到的保号性? - 知乎
- 素材来自:zhihu.com
- 717 x 811 · jpeg
- 费马定理、罗尔定理、拉格朗日中值定理证明 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 870 x 544 · jpeg
- 费马引理证明 - 哔哩哔哩
- 素材来自:bilibili.com
- 1034 x 750 · jpeg
- 费马引理 - 未完代码 - 博客园
- 素材来自:cnblogs.com
- 1148 x 579 · jpeg
- 费马小定理及其多种证明,质数理论的基础 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 2064 x 1290 · jpeg
- 【高等数学第十三讲】中值定理(一)——费马引理 - 哔哩哔哩
- 素材来自:bilibili.com
- 1121 x 858 · jpeg
- 微积分每日一题2-53:费马引理与拉格朗日中值定理的证明题 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 800 x 449 · jpeg
- “费马大定理”不费马,费数学家的脑子!历经358年终于被证明,教育,在线教育,好看视频
- 素材来自:haokan.baidu.com
- 291 x 251 · jpeg
- 人工智能数学基础:费马引理、罗尔定理、拉格朗日微分中值定理、柯西中值定理-CSDN博客
- 素材来自:blog.csdn.net
- 800 x 449 · jpeg
- 费马点,加权费马点,费马点问题模型,原理性质证明,教育,在线教育,好看视频
- 素材来自:haokan.baidu.com
- 1018 x 660 · png
- 几何光学学习笔记(2)- 1.2 费马原理、马吕斯定律和成像_几何光学马吕斯定律怎么理解-CSDN博客
- 素材来自:blog.csdn.net
- 220 x 197 · jpeg
- 费马原理_360百科
- 素材来自:baike.so.com
- 1920 x 1080 · jpeg
- 费马猜想有哪些?为什么数学家们花了数百年时间去证明? - 知乎
- 素材来自:zhuanlan.zhihu.com
- 720 x 2252 · jpeg
- 3.2.3.3费马引理 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1975 x 2760 · jpeg
- 费马大定理手稿,马大定理,马大定理图片_大山谷图库
- 素材来自:dashangu.com
- 833 x 384 · png
- 微分中值定理(一)-CSDN博客
- 素材来自:blog.csdn.net
- 724 x 494 · jpeg
- 费马小定理图册_360百科
- 素材来自:baike.so.com
- 1904 x 2500 · jpeg
- 第三章 微分中值定理与导数的应用 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 素材来自:v.qq.com
- 873 x 436 · jpeg
- 用费马原理证明折射定律 - 哔哩哔哩
- 素材来自:bilibili.com
- 935 x 619 · png
- 费马大定理 - 搜狗百科
- 素材来自:baike.sogou.com
- 1547 x 2107 · png
- 费马大定理的一种证明方法_文档下载
- 素材来自:doc.xuehai.net
随机内容推荐
宠物护理
教育研究与实验
猫简笔画图片大全
北大就业指导中心
体癣初期图片
午门斩首
近视度数对照表
座椅通风
微粒贷怎么开通
宁波婚纱照
森林之子
拳击吧
钓鱼人渔具
pestle
本田圭佑
男人穿女装
复仇三部曲
中国屈辱史
灵机文化
企业5s管理培训
春之文祭
大二能考研吗
老男人头像
水浒传梗概
三级管
红酒瓶
峰谷电价
上海达丰电子厂
七七节
孝顺父母的图片
客户开发
黄家驹专辑
sph
博奥晶典
犹太人的教育
泡泡龙
世界上最大的狮子
白起怎么玩
表白怎么说
关于金钱的名言
聚酯纤维和涤纶
东华帝君是谁
怎么申请留学
作文主题
dfc
压缩板
dmall
低开高走
pvsyst
全年资料
48个音标
零号身材
鼠尾草酸
瑜伽培训
炼金石
营养成分表
桂林自助游攻略
兵长
繁转简
委内瑞拉地图
八字命局
党选拔干部坚持
老师我爱你手抄报
无源晶振
中秋节ppt
南极中山站
个人简历照片
ca998
折射定律
看笑话
镇远县
学美甲有前途吗
滁州长城影视基地
北京壹号院
网关ip
资源配置
略阳
亲近母语
肺在哪个位置图
林达尔均衡
大英博物馆图片
64卦详解
碳排放权交易
黄帝陵图片
泰康人寿怎么样
低钠
如何煲耳机
托马斯的故事
b模
1公分是多少厘米
婚戒图片
贝多芬第三交响曲
战诗
qidong
物料需求计划
实体法
透天厝
中考语文作文题目
dnscrypt
厦门植物园
法国运动品牌
梅长苏
晚会节目单
声乐歌曲
中秋手抄报图
小比熊图片
官场情妇
1984
白色背景图片全白
心理学小游戏
柏拉图多面体
格里高利圣咏
47中
冲床维修
玄关灯
机动车过户
英镑标志
猪图片
刘裕北伐
韩国国歌
五月天玛莎
罗四海
四面佛图片
hello树先生
苏联战争
数学期望公式
拳皇克拉克
必应图片
图坦卡门
美国凯斯西储大学
塔玛拉
是不
散文投稿
泉州东湖公园
陈伯
内涵外延
双色球规则
土狗
世界金融中心
阴到图片
木心美术馆
裸贷是什么意思
相对主义
美缝价格
职业指导
鞌之战
刘安杀妻
无题原文
古诗文
天使泪
有意味的形式
死海文书
企鹅tv
雷神图片
绣春刀图片
便利店发展
鲁宾
苏格拉底的爱情
快递怎么收费
魔方二层公式
四线三格
南门口
恋爱定律
磁盘分区怎么合并
中心体
冥王计划
矩形截面惯性矩
年画娃娃图片
吸附等温线
农村适合开什么厂
罗盘指南针
lol厂长
黄花梨手串图片
绞刑是什么
舞蹈组合
pjm
日在校园
面对巨人
野马汽车标志
移动国际漫游
恋人电影
上吊
消防报警主机
多项式除法
如何学习
着魔电影
冻土
避孕凝胶
改编古诗
lol厂长
解放军占领巴黎
邦尼尔弹簧
易神
百度魏则西事件
海子自杀
菩提老祖的来历
铁血联盟
玫瑰茄图片
演歌
连州
今日热点推荐
泰国坠崖孕妇被指责生意做太大
腾讯回应微信提现可免手续费
这样的文物戏精亮了
四大扛剧女演员
音乐节主办停止和周密合作
卖鱼哥放弃满车鱼虾泼1吨水救人
傅首尔回应傅首尔面相
李行亮团队婉拒采访
国产老剧被AI爆改得像中毒了
撞死知名医生肇事者家属请求谅解
这样使用避孕套是无效操作
TREASURE将换队长
丁禹兮今天喝奶茶啦
王安宇好帅
23岁清华女博士对人生的真实感受
美国小伙说来北京像到了公元3000年
90多名艾滋病患儿有个共同的家
台湾情侣被曝吸毒后打死1岁女儿
半夜天花板上掉下一只300斤野猪
多多佳鑫
唐嫣罗晋带娃逛迪士尼
颜如晶瘦了55斤解锁全新风格
李行亮商演再次遭抵制
微信提现可以免手续费了
向鱼深V
央视曝光学生体育用品中的增塑剂
老人摔倒瞬间大哥滑铲接住头部
刘宪华演唱会
陈哲远举125公斤杠铃
赵雅芝哭了
迪丽热巴陈飞宇公主抱路透
华晨宇蹦丢了一个31万的耳钉
孙红雷关晓彤张艺兴好先生友谊
蒋敦豪交给时间解答
叙利亚
孕妇想月子期间洗头被长辈包围劝阻
无畏向鱼终于加微信了
曼联vs埃弗顿
国考笔试实际参考258.6万人
皇马vs赫塔菲
朱志鑫剪头发
我是刑警半枚血指纹破案
张泽禹发了18宫格
陈小春看到梅艳芳的身影哭了
言语缩减
白桃星座
女子花近五万相亲三次都失败盼退费
泰国孕妇坠崖案双方仍未离婚
全圆佑绝美氛围
利物浦vs曼城
【版权声明】内容转摘请注明来源:http://maijichuang.cn/9wj6k1_20241126 本文标题:《费马引理最新视觉报道_费马引理的通俗理解(2024年12月全程跟踪)》
本站禁止使用代理访问,建议使用真实IP访问当前页面。
当前用户设备IP:3.15.31.27
当前用户设备UA:Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko; compatible; ClaudeBot/1.0; +claudebot@anthropic.com)